
モンティ・ホール問題とはモンティ・ホールが司会を務めるゲームショー番組で出題された、とある確率論に関するクイズ問題です。
小中学生でも理解できるくらいシンプルな問題。だけどどんなに高学歴で頭の良い人でも直感で答えたらほぼ間違えるという面白い問題です。著名な数学者ですら間違えて大騒動に発展したくらいですからね。
モンティ・ホール問題は理解できない人は何回説明されても理解できないものです。しかし実はそれは理解力に問題があるのではなく、十中八九モンティ・ホール問題の厳密なルールをきちんと把握できていないのだと思います。
ルールの解釈次第で答えが変わってくるというのが一番厄介なところ。そして簡略化されたモンティ・ホール問題ではそのルールについてきちんと説明されていないのです。
しかしモンティ・ホール問題のルールをきちんと把握してしまえば中学生レベルの数学を修めていれば理解できるでしょう。
目次
モンティ・ホール問題とは?
まずはモンティ・ホール問題とはどういう問題なのか説明していきます。
これを読んでいる人はすでにモンティ・ホール問題について知っている人がほとんだと思うので、そういう場合は飛ばして構いません。
ドアA、ドアB、ドアCにはそれぞれヤギ、ヤギ、車がランダムで入っており、プレーヤーに車が入っているドアを当てさせます。

まずプレーヤーがドアを一つ選びます。

次に司会者のモンティは残りのドアの内ヤギが入っているドアを開けます。
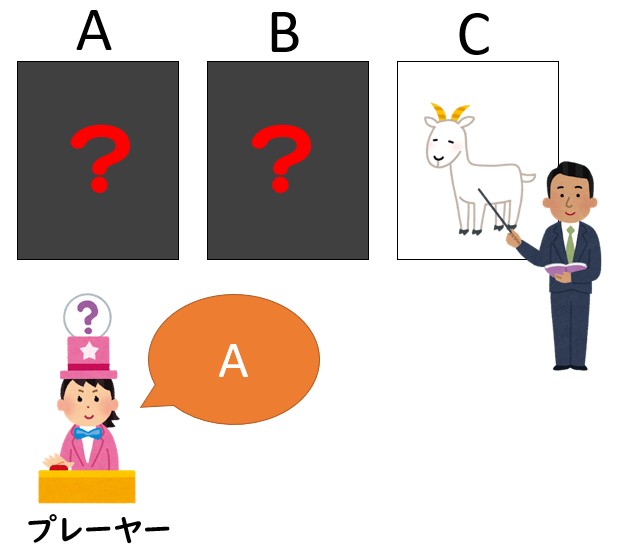
そしてモンティはプレーヤーにドアを変更しても良いと言います。

この時、プレーヤーはドアを変更するべきかどうか?
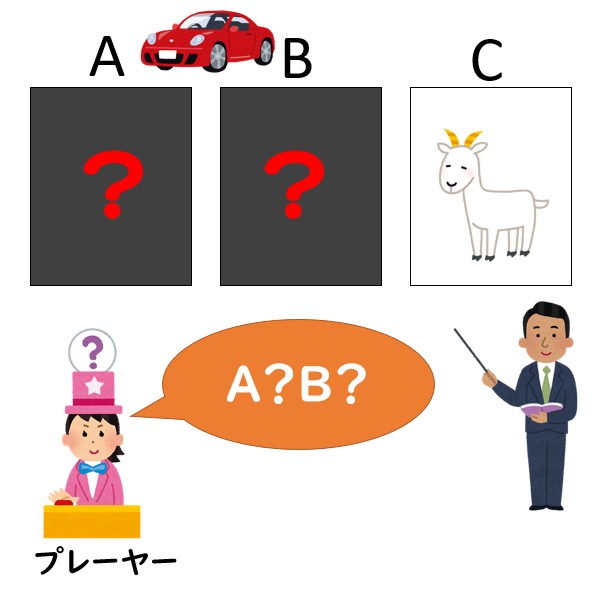
これがモンティ・ホール問題です。
直感的に考えれば変更してもしなくても確率は1/2。実際にプレーヤーの立場で考えれば変更可能と言われると誘導されているように思えてしまうので、変更したくない人が多いでしょう。
しかし、実はプレーヤーがドアを変更しなければ当たりの確率が1/3であるのに対し、変更したら2倍の2/3になるのです。

つまり「変更するべき」というのが答えです。
モンティ・ホール問題は最近ではいろんなテレビやアニメなどで取り扱われることもあり知名度が増してきましたし、この問題の解説もいろいろあります。
しかし人によっては何回説明されても「なぜ変更したら確率が上がるのか」が理解できない人も多いです。
ただその原因はその人に理解力がないというのではなく、モンティ・ホール問題の厳密なルールが省かれていることが原因であることがほとんどだと思います。
モンティ・ホール問題の簡略化されたルールの場合、解釈次第では答えが変わってしまいますからね。
私自身、いろんなサイトを見たり色んな人に聞いたりしても理解できませんでしたが、モンティ・ホール問題のルールをきちんと把握したらすぐに分かりました。
では解説に入ります。
中学生でもわかるモンティ・ホール問題の解説
最も重要な前提ルールの把握
モンティ・ホール問題はわかりやすさ重視の簡略化されたルールがミスリードを誘っているという場合が多いので、まずはモンティ・ホール問題の厳密なルールを見てみましょう。
- ドアにはヤギ、ヤギ、車がランダムで入っている
- プレーヤーがドアを1つ選択する
- モンティは残りの2つのドアをのうち1つを必ず開ける
- モンティが開けるドアには必ずヤギが入っている
- モンティはプレーヤーにドアの選択を変更するかどうかを尋ねる
- プレーヤーは上記のルールを把握している
特に重要なのは「3」「4」「6」。
つまりこういうことです。
- 「モンティがドアを開けること」はあらかじめルールとして決まっている
- モンティが開けるのは「プレーヤーが選んでいないハズレのドア」
- プレーヤーは「モンティがドアを必ず開けること」や「開けるドアの条件」を把握している
このモンティがドアを開けるルールの解釈によって答えが変わってくるのがモンティ・ホール問題の厄介なところ。正直このルールが明記されていなければ問題は成り立たないと思います。
プレーヤー視点で考えれば、「モンティが後出しでルールを追加した」「モンティは無作為で選んだドアがヤギだった」と誤解しがち。
一番大事なのは『「モンティがドアを開けるのはルールーの一環であり、プレーヤーが選んでいないヤギのドアを意図的に開けた」というのをプレーヤーが把握していること』です。
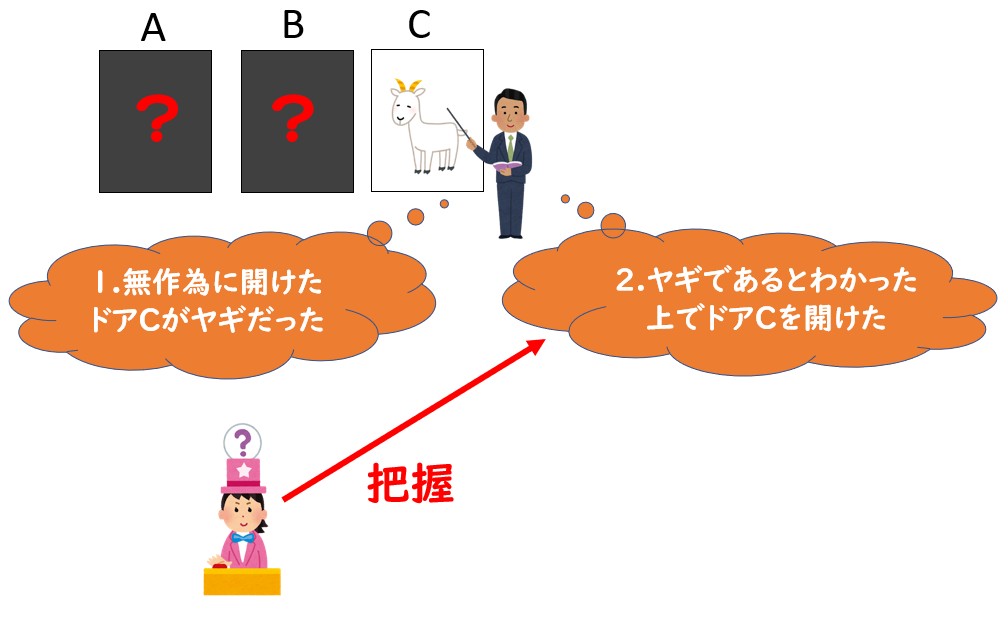
モンティ・ホール問題が理解できない人はこれを見落としている可能性が高いです。
もしもモンティが無作為にドアを開けたと勘違いしていたら、「変更してもしなくても確率は変わらない」というのが答えになってしまいます。
では前提となるルールを確認したところで、解説に入っていきます。
モンティ・ホール問題の感覚的な解説
モンティ・ホール問題において「変更してもしなくても確率は1/2」と考えてしまう理由は、直感的に“最初に選んだドア”と“残ったドア”が同じ条件の同価値のドアに思えてしまうからです。
この間違った直感的な認識を正すために、感覚的な話をします。
ルールをきちんと把握できれば残った2つのドアが異なる価値のものだと分かるでしょう。
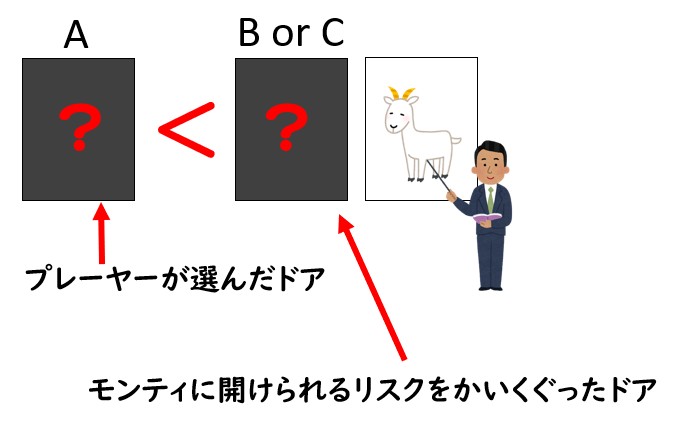
たとえばドアAをプレーヤーが選択すれば、「ドアA」と「ドアBまたはドアC」が残ります。
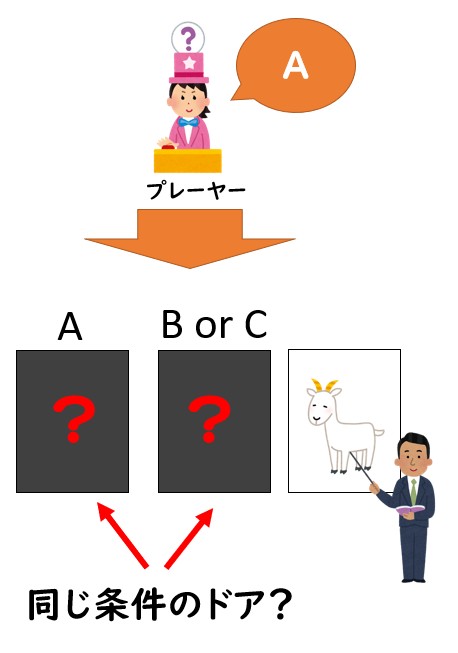
ドアAは「プレーヤーが選んだから残っているドア」であるのに対し、もう一方のドアは「モンティに開けられる可能性があったドア」です。
感覚的な説明をすれば、「プレーヤーが選んだ以上無条件で残るドアA」と「開けられるリスクをかいくぐったドア」が同価値ではないというのはなんとなく分かるのではないでしょうか。
これだけではわからない人も多いと思うので、具体的に見てみましょう。
具体的に場合分けを用いた解説
最初にプレーヤーがAを選んだ時、どこに車が入っているかで正解となる選択を場合分けしました。
| パターンA | パターンB | パターンC | |
|---|---|---|---|
| 当たり (車のドア) | A | B | C |
| モンティが開けるドア | BまたはC(50%) | C | B |
| 最後に残るドア | 「A」、「BまたはC(50%)」 | 「A」、「B」 | 「A」、「C」 |
| 変更する場合に選択するドア | BまたはC(50%) | B | C |
| 車を選ぶ選択 | 「変更しない」 | 「変更する」 | 「変更する」 |
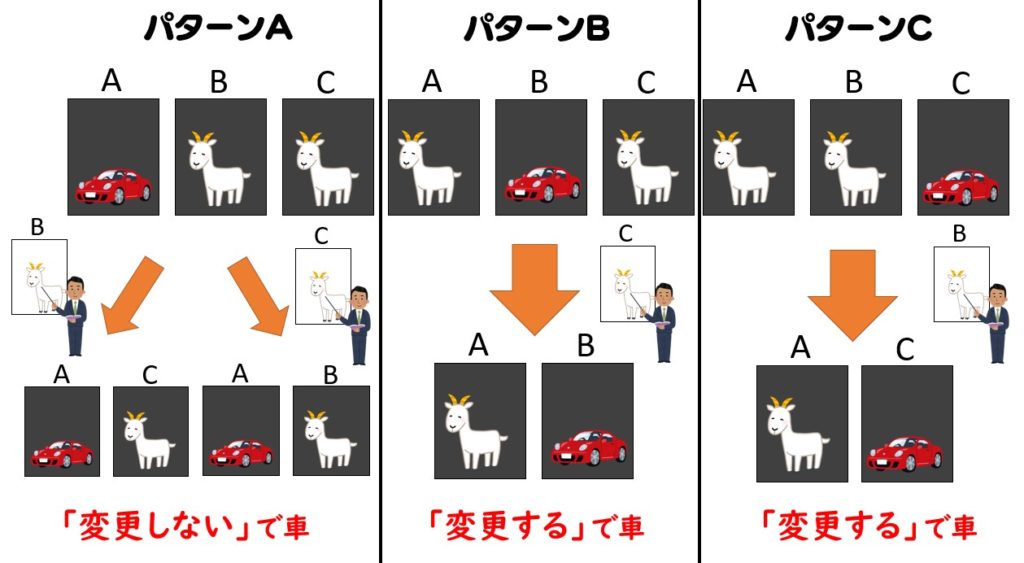
3通りのパターンがありますが、「変更しない」で車を選択するのが1通りなのに対し、「変更する」で車を選択するのは2通り。
結局は最初で選んだ1つか、それとも選んでいない残りの2つかどちらにかけるかなので確率はそれぞれ1/3と2/3になります。
はじめのプレーヤーの選択は単なる組分けと考える
モンティ・ホール問題は最初のプレーヤーの選択を単なる組分けだと考えて、最後にプレーヤーがドアの選択するというルールで解釈すると意外とすんなり理解できるものです。
- プレーヤーは3枚のドアの内、1枚と2枚の組に分ける
- モンティは2枚の組の内ハズレのドアを1枚排除する
- プレーヤーはどちらを選択するべきか?



1枚の組を選択する場合は、本来の「変更しない」という選択、2枚の組の側のドアを選択する場合は「変更する」という選択になります。
結局は「最初に分けた1つと2つの組のドア、どちらにあたりが入っているか?」という問題になるのです。

ルールの本質は変わっていませんが、こういうルールと解釈するなら直感的にも理解しやすいのではないでしょうか。
極端な例(膨大な数のドア)で考える
複雑な問題が理解できない場合、極端な例で考えてみるとすんなり分かることがあります。
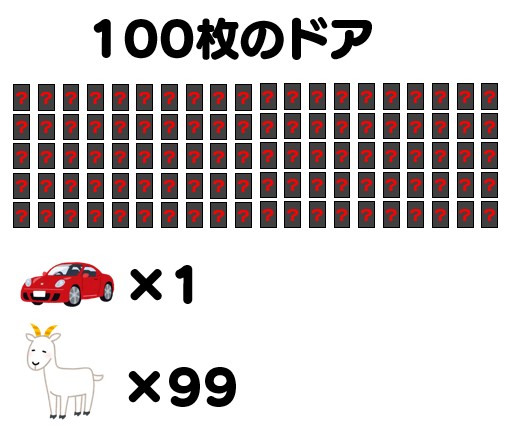
ここではドアの数を100枚にしてみましょう。当たりのドア1枚、ハズレのドア99枚です。
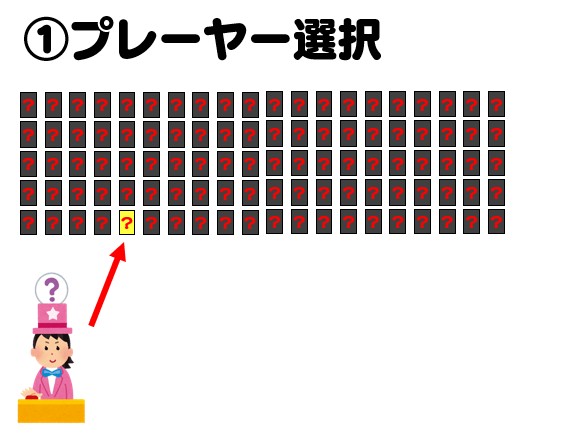
まずプレーヤーは100枚のドアのうち1枚を選びます。
続いて、司会者はプレーヤーが選択したドアを残して、ハズレのドアを98枚開けて残り2枚にします。
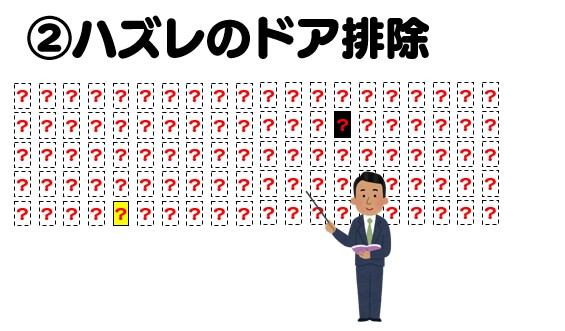
最後にプレーヤーはドアを変更するべきでしょうか?
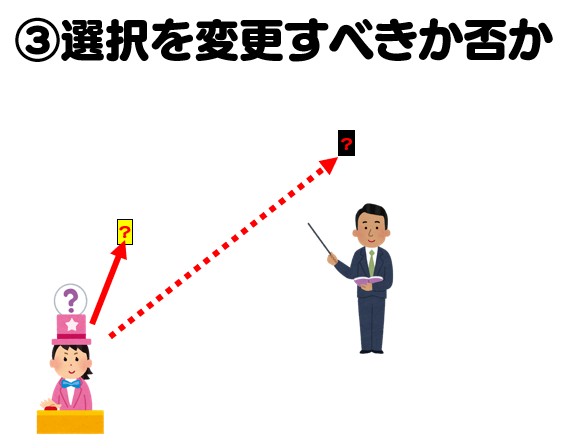
最初にプレーヤーが当たりのドアを選択していれば「変更しない」で車が当たりますが、ハズレのドアを選択していたら「変更する」で車が当たります。
つまり「変更しない」で当たる確率は1/100であるのに対し、「変更する」だと99/100で当たりです。
あとがき
以上、モンティ・ホール問題の解説でした。
繰り返しますが、これを理解できるかどうかは理解力の問題と言うよりも、ルールを正しく把握しているかどうかというところにあります。
モンティ・ホール問題は著名な数学者ですら正解を認められずに激しく反論して大騒動になりましたが、その原因はルールを誤認していたことにありますからね。
言及されなくても問題の趣旨をきちんと把握するのが大事という意味では、頭の良さや理解力が大事と言えるかもしれませんが。
それでは最後までご覧いただきありがとうございました。